数量关系

一、数学推理

1、平方根，又叫二次方根，表示为〔±√￣〕，一个正数有两个实平方根，它们互为相反数，负数没有平方根，0的平方根是0。

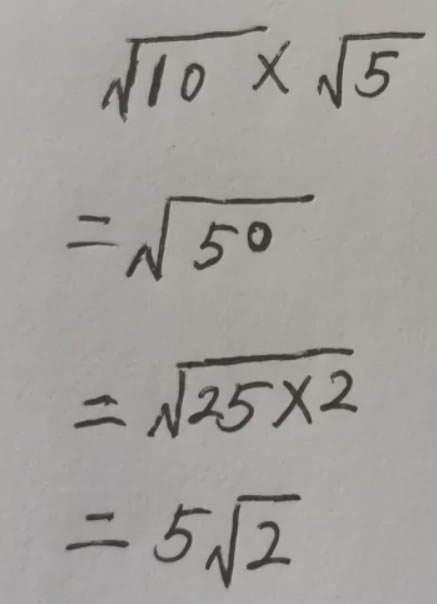
2、数列规律：

（1）有分数：全部转分数，（可化简）再分析分母等差，分子等差

（2）数列起伏大：①考虑倍数关系；②或者圈前面三个数，做运算。

（3）数列起伏小：①考虑作差关系，前后差得到新数列（可两次做差），再计算；②前后两项相加，得到新数列，再计算

（4）多位数无规律、小数点：考虑机械划分，数字拆开，做加减法

(5)数列有大有小:相邻三位数有商、积关系。

二、数学运算

（1）列分程式

公约数就是可以被同一个数整除的,例如2,3,4是12的公约数,

公倍数就是可以整除某些数,就是这些数的公倍数,36是2,3,4,6的公倍数

一.行程问题

1、基本公式：路程=速度×时间，等时间平均速度=，等距离平均速度=。

2、相遇和追及

路程和=速度和×时间

直线上，两人同时出发相向而行时，第n次相遇时，(2n-1)S=(V1+V2)t

环形上，两人同时出发背向而行，第n次相遇是，路程和=nS=(V1+V2)t

直线上，两人同时出发同向而行，路程差=速度差×时间

环形上，两人同时出发同向而行，第n次追上，路程差=nS=(V1-V2)t

3、流水行船

顺水速度=船速+水速

逆水速度=船速-水速

顺水速度+逆水速度=2×船速

顺水速度-逆水速度=2×水速

4、火车过桥

路程=桥长+车长

二.工程问题

1、工作总量=工作效率×工作时间

2、合作效率=多个人的效率之和

3、合作总量=合作效率×工作时间

4、工程问题常用方法：

方程法

比例法：路程一定，速度和时间成反比关系;速度一定，路程和时间成正比;时间一定，路程和速度成正比。

赋值法：W、P、T至多只给一个实际量。已知同一项工程的多个完工时间，给工作总量赋值，赋为时间的最小公倍数，进而表示出效率;已知效率比给效率赋值，直接赋为比例值即可。

周期循环式工作：

计算一个周期的时间和一个周期中的工作量

计算需要几个周期

分配余下工作

三.浓度问题

1、溶液=溶质+溶剂

2、浓度=溶质÷溶液

3、混合浓度=混合前溶质的和÷混合前溶液的和=(溶质1+溶质2)÷(溶液1+溶液2)

4、巧用“十字交叉法”解决混合溶液问题，解题核心为差之比=溶液质量之比。

四.经济利润问题

1、售价=成本+利润

2、利润率=

3、售价=成本×(1+利润率)

4、折扣=折后售价/折前售价

五.排列组合

(1)排列

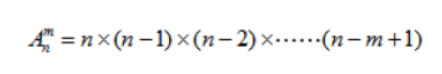
(2)组合

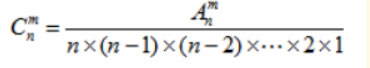
2.常用方法：

捆绑法(相邻)：第一步，把相邻元素捆在一起当做一个整体参与排列;第二步，再考虑整体内部顺序。

插空法(不相邻)：第一步，先安排其他元素，再把不相邻元素插入其他元素形成的空中。

间接法(直接考虑复杂，考虑反面)：所求情况数=总的情况数—反面情况数。

3.隔板法：把n个相同物品分给m个人，每人至少一个，共有种方式。

4.错位排列：2个元素的错位排列有1种，3个元素有2种，4个元素有9种，5个元素有44种。